Двоичная система счисления имеет основание р

СИСТЕМЫ СЧИСЛЕНИЯ И КОДЫ, ПРИМЕНЯЕМЫЕ В ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКЕ

Системой счисления (с.с.) называется способ представления чисел посредством цифровых знаков.

В качестве цифровых знаков используются арабские и римские цифры.

Системы счисления делятся на позиционные и непозиционные.

Примером непозиционных с.с. может служить римская или латинская с.с. Она включает в себя следующие цифровые обозначения: 1 – I; 2-II; 3-III; 4-IV; 5-V; 10-X;…; 50-L; 100-C; 500 — D; 1000-M и т.д.

Пример 3.Записать числа 114; 155; 1999 римскими цифрами:

114 — CXIV; 155 — CLV; 1999 — MCMXCIX.

В виду сложности не нашла своего применения в математике.

В позиционной с.с. с основанием p числа представляются в виде последовательности цифровых знаков:

Основание системы счисления – это количество цифр используемых для формирования данной системы счисления.

В зависимости от основания системы счисления различают:

· десятичную с.с. (0, 1, 2, 3, 4, 5, 6, 7, 8, 9);

· двоичную с.с. (0, 1);

· восьмеричную (0, 1, 2, 3, 4, 5, 6, 7);

· шестнадцатеричную (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F) .

В этих системах значение цифры определяется местом (позицией), где она стоит в числе

Пример 4.6321(10) = 6 3 2 1 = 6*10 3 +3*10 2 +2*10+1

каждую позицию цифры в числе принято оценивать «весом» показателем степени системы счисления. В первой справа пози­ции размещаются единицы (для целого числа), в соседней с ней второй позиции – десятки, в третьей – сотни, в четвертой — тысячи и т.д. Дробная часть десятичного числа находится справа от десятичной точки, используемой для отделения целой части числа от дробной. Каждая позиция справа от десятичной точки имеет свой вес (10 -1 , 10 -2 и т.д).

В любой позиционной с.с. число может быть записано через полином (многочлен):

где нижние индексы определяют местоположение цифры в числе (разряд):

• положительные значения индексов — для целой части числа (т разрядов);

• отрицательные значения — для дробной (s разрядов).

Пример 5.237,71(10) = 2*10 2 +3*10 1 +7*10 0 +7*10 -1 +1*10 -2

Двоичная система счисления имеет основание Р = 2 и использует для представле­ния информации всего две цифры: 0 и 1.

Существуют правила перевода чисел из одной сис­темы счисления в другую, основанные, в том числе и на соотноше­нии (1).

Пример 6.101110,101(2)=1•25+0•24+1•23+1•22+1•21+0•20+1•2-1+0•2-2+1•2-3=
46,625(10),

т.е. двоичное число 101110,101 равно десятичному числу 46,625. При записи числа в десятичной системе счисления каждая позиция занята десятичной цифрой. Аналогично при записи двоичного числа каждая позиция занята двоичной циф­рой, называемой битом. Часто используется термин –наименьший значащий бит (крайний справа) и наибольший значащий бит (крайний слева).

Преобразование двоичных чисел в десятичные.

При работе ЭВМ часто бывает необходимо заменить двоичные числа их десятичными эквивалентами.

Процедура преобразования двоичного числа в десятичное проста: необходимо сложить десятичные веса всех разрядов двоичного числа, в которых содержаться единицы.

Пример 7.Преобразование вещественного двоичного числа: 101.011 в десятичное:

1 0 1. 0 1 1 = 1*2 2 +0* 2 1 +1* 2 0 +0* 2 -1 + 1*2 -2 +1*2 -3 =5.375(10)

Перевод из одной системы счисления в другую.

1. Для целой части используется правило последовательного деления

2. Для дробной части правило последовательного умножения.

Правило перевода целой части — правило последовательного деления: Для перевода целой части числа из С.С. с основанием p в С.С. с основанием q необходимо разделить целую часть заданного числа и получаемое частное на основание системы в которую необходимо преобразовать данное число, представленное в С.С. p, до тех пор пока частное не станет меньше q.

Старшей цифрой записи числа служит последнее частное, а следующие за ней дают остатки от деления частичных частных. Выписываются в порядке обратном их получения.

таким образом, получили число: (последнее частное) и затем остатки в порядке обратном их получения.

Двоичная система счисления Bin (Вinary)

Пример 8.Преобразовать десятичное число 134 в двоичное:

Частичные частные	Последнее частное
Остатки

Получили число10000110 B

Правило перевода дробной части — правило последовательного умножения: Для перевода правильной дроби из С.С. с основанием p в С.С. с основанием q необходимо умножить исходную дробь и дробные части получающихся произведений на основание системы в которую необходимо преобразовать данное число, представленное в С.С. p. Целые части получающихся произведений дают последовательность цифр представления дроби в С.С. q.

Пример 9.Преобразовать десятичную дробь 0.375 в двоичную

0.375 * 2 = .75 Старший Значащий Разряд(СЗР)

0.75 * 2 = 1.5 1

0.5 *2 = 1 1Младший ЗР (МЗР) Результат 0.011

Восьмеричная система счисления Oct (Оctal)

Восьмеричная система счисления имеет основание 8. В ней используются следующие символы: 0, 1, 2, 3, 4, 5, 6, 7. Восьмеричная система применяется для удобства записи чисел. Поскольку 2 3 = 8, то каждый восьмеричный символ (0 до 7) может быть представлен 3-х битовым числом (000 …..111)

Для перевода двоичного числа в восьмеричную систему счисления необходимо двоичное число разбить вправо и влево от запятой на триады (по три двоичных бита). При необходимости крайнюю левую триаду (целой части) и крайнюю правую (дробной части) дополняют нулями, затем каждую триаду заменяют восьмеричным числом.

Пример 10. Представить восьмеричным эквивалентом число:

10101011111101 ( B )=>25375 ( О )

Двоичный код, разбитый на триады	010 добавлен 0
Восьмеричный код

Для перевода из восьмеричной в двоичную с.с. достаточно заменить каждую цифру восьмеричного числа соответствующим 3-х разрядным двоичным числом. При этом незначащие нули слева от целой части числа, и справа от дробной части отбрасываются.

Пример.11.Представить двоичным эквивалентом число:

375,75 ( O )=>11111101,1111 ( B )

Восьмеричный код	5,
Двоичный	101,

Шестнадцатеричная система счисления Hex (Hexadecimal)

Используются символы: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. (А = 10, В = 11, С = 12, D = 13, Е = 14, F = 15)

Правило перевода шестнадцатеричных чисел в двоичные аналогично вышеизложенному, но используют не триады, а тетрады. Шестнадцатеричную цифру можно представить как средство сокращенной записи 4– х разрядного двоичного числа.

Преобразование двоичных чисел в 16-ные осуществляется по правилам, аналогичным для преобразования их в восьмеричные. Для этого биты целой и дробной частей влево и вправо от запятой группируются по четыре.

Пример 12. Представить шестнадцатеричным эквивалентом:

10101011111101 B => 25375 O => 2AFD H

Двоичный код, разбитый на тетрады
шестнадцатеричный код	А	F	D

11000111.10101 B=>307.52 O => C7.A8 H

Двоичный код, разбитый на тетрады	1000 добавлены нули в конце дробной части
шестнадцатеричный код	С	A
Целая часть	Дробная часть

Следует помнить, что 16-ные и 8-ные числа — это только способ представления двоичных чисел, которыми фактически оперирует микропроцессор.

Простота соотношения между 16 и 2 формами представления чисел – причина значительно большей распространенности 16 с.с.

Пример 13.Преобразование из двоичной системы в 8, 16, 101101.0111

B => 15.34O => D.7H

Пример 14.Преобразование из восьмеричной системы в 10, 16

1172.25O => D; 634.328125 D => H,

ответ: 1172.25 O=>634.328125 D=>27A.54 H

Системы счисления

Разнообразные системы счисления, которые существовали раньше и ко­торые исполь­зуются в наше время, можно разделить на непозиционные и по­зиционные. Знаки, ис­поль­­зуемые при записи чисел, называются цифра­ми.

В непозиционных системах счисления от положения цифры в записи числа не зави­сит величина, которую она обозначает. Примером непозицион­ной системы счисления яв­ляется римская система, в которой в качестве цифр используются латинские буквы:

1 5 10 50 100 500 1000

Например: VI = 5 + 1 = 6, а IX = 10 — 1 = 9.

Недостатки непозиционных систем счисления:

1) для записи больших чисел требуется вводить новые обозначения, которых будет все больше и больше;

2) непонятно, как записывать дробные и отрицательные числа

3) Не существует алгоритмов выполнения арифметических операций

В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от ее места в числе (позиции). Позиция цифры в числе называется разрядом. Разряд числа возрастает справа налево, от младших разрядов к старшим.

Основанием позиционной системы счисления называется число, которое показывает, во сколько раз изменяется значение цифры при перемеще­нии ее на 1 разряд вправо или влево. Основание системы счисления равно количест­ву цифр в этой системе. счисления. Первая известная нам система, основанная на позиционном принципе — шестидесятеричная вавилонская. Цифры в ней были двух видов, одним из которых обозначались единицы, другим — десятки. Следы вавилонс­кой системы сохранились до наших дней в способах измерения и записи ве­ли­чин углов и промежутков времени.

Однако наибольшую ценность для нас имеет индо-арабская десятичная система. Индийцы первыми использовали ноль для указания позиционной зна­чимос­ти величины в строке цифр. Эта система получила название де­ся­тич­ной, так как в ней десять цифр.

Для того чтобы лучше понять различие позиционной и непозиционной систем счисления, рассмотрим пример сравнения двух чисел. В позиционной системе счисления сравнение двух чисел происходит следующим образом: в рассматриваемых числах слева направо сравниваются цифры, стоящие в оди­наковых позициях. Большая цифра соответствует большему значению числа. Например, для чисел 123 и 234, 1 меньше 2, поэтому число 234 больше, чем число 123. В непозиционной системе счисления это правило не действует. Примером этого может служить сравнение двух чисел IX и VI. Несмотря на то, что I меньше, чем V, число IX больше, чем число VI.

Далее мы будем рассматривать только позиционные системы счисления.

Основание системы счисления, в которой записано число, обычно обоз­на­­чается нижним индексом. Например, 555₇ — число, записанное в семе­рич­ной системе счисления. Если число записано в десятичной системе, то осно­вание, как правило, не указывается. Основание системы — это тоже число, и его мы будем указывать в обычной десятичной системе. Вообще, число X в системе счисления с основанием q означает значение многочлена:

где a_n. a — цифры в представлении данного числа.

Значения цифр изменяются от 0 до q-1.

1235₁₀ =1*10 3 + 2*10 2 + 3*10 1 + 5*10 0

1235₈ =1*8 3 + 2*8 2 + 3*8 1 + 5*8 0 = 1* 512 + 2*64 + 3*8 + 5 = 669₁₀

1101₂ = 1*2 3 + 1*2 2 + 0*2 1 + 1*2 0 = 8 + 4 + 1 = 13₁₀

B6₁₆ = 11*16 + 6 = 176 + 6 = 182₁₀

Обратите внимание на то, что чем больше основание системы счисле­ния, тем больше число, записанное определенной последовательнос­тью цифр, например: 1235₁₀ > 1235₈, но однозначные числа (состоящие из одной цифры) имеют одно и то же значение во всех системах счисления: 5₁₀ = 5₈.

Наибольший интерес при работе на ЭВМ представляют системы счис­ле­ния с основаниями 2, 8 и 16. Вообще говоря, этих систем счисления обыч­но хватает для полноценной работы как человека, так и вычислительной маши­ны. Однако иногда в силу различных обстоятельств все-таки приходится об­ращаться к другим системам счисления, например к троичной, семеричной или системе счисления по основанию 32. Для того чтобы нормально оперировать с числами, записанными в таких нетрадиционных системах, важно понимать, что принципиально они ничем не отличаются от привычной нам десятичной. Сложение, вычитание, умножение в них осуществляется по одной и той же схеме.

В вычислительных же машинах используется двоичная система счис­ле­ния, так как оперировать с числами, записанными в двоичном виде, до­воль­но просто. Часто в информатике используют шестнадцатеричную систему, так как запись чисел в ней значительно короче записи чисел в двоичной системе. Может возникнуть вопрос: почему бы не использовать для записи очень боль­ших чисел систему счисления, например по основанию 50? Для такой системы счисления необходимы 10 обычных цифр плюс 40 знаков, которые соответствовали бы числам от 10 до 49 и вряд ли кому-нибудь понравится работать с этими сорока знаками. Поэтому в реальной жизни системы счис­ления по основанию, большему 16, практически не используются.

Следует отметить, что большинство калькуляторов, реализованных на ЭВМ (в том числе и Calc), позволяют осуществлять работу в системах счис­ления с основаниями 2, 8, 16 и, конечно, 10.

Двоичная система счисления

Люди предпочитают десятичную систему, вероятно, потому, что с древ­них времен считали по пальцам. Но, не всегда и не везде люди пользовались десятичной системой счисления. В Китае, например, долгое время приме­ня­лась пятеричная система счисления. В ЭВМ используют двоичную систему потому, что она имеет ряд преимуществ перед другими:

· для ее реализации используются технические элементы с двумя воз­можными состояниями (есть ток — нет тока, намагничен – ненамагни­чен);

· представление информации посредством только двух состояний на­деж­но и помехоустойчиво;

· возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;

· двоичная арифметика проще десятичной (двоичные таблицы сложения и умножения предельно просты).

В двоичной (binary) системе счисления всего две цифры, называемые дво­ичны­ми (binary digits). Сокращение этого наименования привело к появлению тер­мина бит, ставшего наз­ванием разряда двоичного числа. Веса разрядов в дво­ичной системе изменяются по степе­ням двойки. Поскольку вес каждого раз­ря­да умножается либо на 0, либо на 1, то в резуль­тате значение числа опреде­ляется как сумма соответствующих значений степеней двойки. Если какой-ли­бо разряд двоичного числа равен 1, то он называется значащим разрядом. За­пись числа в двоичном виде намного длиннее записи в десятичной системе счисления.

Арифметические действия, выполняемые в двоичной системе, подчиня­ют­ся тем же правилам, что и в десятичной системе. Только в двоичной сис­теме перенос единиц в старший разряд возникает чаще, чем в десятичной. Вот как выглядит таблица сложения в двоичной системе:

0 + 0 = 0 0 + 1 = 1

1 + 0 = 1 1 + 1 = 10 (перенос в старший разряд)

Таблица умножения для двоичных чисел еще проще:

0 * 0 = 0 0 * 1 = 0 1 * 0 = 0 1 * 1 = 1

Пример выполнения операции сложения в двоичной системе счисления:

1 0 1 1₂ Красным цветом показан перенос из младших разрядов в

Для проверки правильности выполнения операции переведем все три чис­ла из двоичной системы в 10-ую:

1011 = 1*2 3 + 1*2 1 + 1 = 8 + 2 + 1 = 11₁₀

110 = 1*2 2 + 1*2 1 = 4 + 2 = 6₁₀

10001 = 1*2 4 + 1 = 16 + 1 = 17₁₀

Сумма первых двух чисел (11 и 6) равна третьему числу (17), следователь­но операция выполнена верно.

Обратите внимание на то, что при добавлении к числу, состоящему из еди­ниц (11…1), еще одной единицы, получается число, равное 1 с количест­вом нулей, равным количеству единиц исходного числа, например:

1111 1111₂ + 1 = 1 0000 0000₂ = 2 8

Пример выполнения операции вычитания в двоичной системе счисле­ния:

Вычитание выполняется по тем же правилам, что и в 10-ой системе, но в 10-й системе при замене единицы старшего разряда она превращается в 10 еди­­ниц младшего разряда, а в 2-й системе – в 2 единицы. Если нужно про­извести заем не в соседнем разряде, а далее влево, то из каждых двух единиц текущего разряда одна остается в этом разряде, а вторая передается вправо. Сравните:

9 9 9₁₀ 1 1 1₂

Выполним в 2-й системе счисление вычитание 17₁₀ – 6₁₀ :

1 0 1 1₂ = 11₁₀ Проверка показывает, что вычитание выполнено верно.

Если в двоичной системе счисления из числа, являющегося степенью двойки, вычесть 1, то получается число, состоящее из единиц, количество которых равно количеству нулей двоичного числа, например:

2 8 — 1 = 1 0000 0000₂ – 1 = 1111 1111₂

1023 = 1024 – 1 = 2 10 – 1 = 11 1111 1111₂

Пример выполнения операции умножения в двоичной системе счисле­ния:

1 0 0 0 0 0 1₂ = 2 6 +1 = 64 +1 =65₁₀ ( 13 * 5 = 65)

Рассмотрим подробнее, как процессор выполняет умножение двоичных чисел. Пусть надо умножить число 1101 на 101 (оба числа в двоичной сис­теме счисления). Машина де­лает это следующим образом: она берет число 1101 и, если первый справа элемент второго множи­теля равен 1, то она за­носит его в сумму. Затем сдвигает число 1101 влево на одну позицию, полу­чая тем самым 11010, и, если, второй элемент второго множителя равен еди­нице, то добавляет его к сумме. Если элемент второго множителя равен ну­лю, то сумма не изменяется. Этот процесс сдвигов и сложений повторяется.

Пример выполнения операции деления в двоичной системе счисле­ния:

Двоичное деление основано на методе, знакомом вам по десятичному де­ле­нию, т. е. сводится к выполнению операций умножения и вычитания. Вы­пол­нение основной процедуры — выбор числа, кратного делителю и пред­наз­наченного для уменьшения делимого, здесь проще, так как таким числом мо­гут быть только либо 0, либо сам делитель.

В качестве примера разделим 143₁₀ = 10001111₂ на 13₁₀ = 1101₂

1 0 0 0 1 1 1 1 1 1 0 1

— 1 1 0 1 1 0 1 1₂ = 11₁₀

1 0 0 1 1

— 1 1 0 1

Проверка показывает, что деление выполнено верно (143 / 13 = 11).

Умножение или деление двоичного числа на 2 приводит к перемещению запятой, отделяющей целую часть от дробной на один разряд соответственно вправо или влево:

Ая система счисления

При наладке аппаратных средств ЭВМ или создании новой программы возникает необходимость "заглянуть внутрь" памяти машины, чтобы оценить ее текущее состояние. Но там все заполнено длинными последователь­нос­тя­ми нулей и единиц двоичных чисел. Эти последовательности очень неудобны для восприятия человеком, привыкшим к более короткой записи десятичных чисел. Кроме того, естественные возможности человеческого мышления не позволяют оценить быстро и точно величину числа, представленного, напри­мер, комбинацией из 16 нулей и единиц.

Для облегчения восприятия двоичного числа решили разбивать его на группы разрядов, например, по три или четыре разряда. Эта идея оказалась очень удачной, так как последовательность из трех бит имеет 8 комбинаций, а последовательность из 4 бит — 16. Числа 8 и 16 являются степенями двойки, поэтому легко находить соответствие с двоичными числами. Развивая эту идею, пришли к выводу, что группы разрядов можно закодировать, сократив при этом длину последовательности знаков. Для кодировки трех битов требу­ется восемь цифр, поэтому взяли цифры от 0 до 7 десятичной системы. Для кодировки же четырех битов необходимо шестнадцать знаков; для этого взя­ли 10 цифр десятичной системы и 6 букв латинского алфавита: A, B, C, D, E, F. Полученные системы, имеющие основания 8 и 16, назвали соответственно восьмеричной и шестнадцатеричной.

В восьмеричной (octal) системе счисления используются восемь раз­лич­ных цифр: 0, 1, 2, 3, 4, 5, 6, 7. Основание системы — 8. При записи отрица­тель­ных чисел перед последовательностью цифр ставят знак минус. Сло­же­ние, вычитание, умножение и деление чисел, представленных в восьмерич­ной системе, выполняются весьма просто, подобно тому, как это делают в общеизвестной десятичной системе счисления.

Пример выполнения операции сложения в восьмеричной системе счис­ления:

1 1 Красным цветом показан перенос из младших разрядов в старшие.

4 7 6 Выполнение операции в каждом разряде:

+ 3 4 1) 6 + 4 = 10 = 1*8 + 2 = 12₈

5 3 2 2) 1 + 7 + 3 = 1*8 + 3 = 13₈

Проверим результат путем перевода чисел в десятичную систему счис­ления :

476₈ = 4*8 2 + 7*8 + 6 = 318 318

532 = 5*8 2 + 3*8 + 2 = 346 346

Пример выполнения операции вычитания в восьмеричной системе счис­ления:

7 8 Красным цветом показан перенос из старших разрядов в младшие.

5 3 2 Выполнение операции в каждом разряде:

— 3 4 1) 8 + 2 – 4 = 6

4 7 6 2) 7 + 2 — 3 = 1*8 + 3 = 13₈

Пример выполнения операции умножения в восьмеричной системе счис­ле­ния:

5 4 54 4*4 = 16 = 2*8 + = 20₈ (записываем 0)

2 3 2 0 54 4*3 = 12 = 1*8 + 4 = 14₈ (записываем 4)

2320₈ = 2*8 3 + 3*8 2 + 2*8 = 1232₁₀ 352

Пример выполнения операции деления в восьмеричной системе счис­ле­ния:

2 3 2 0₈ 5 4₈

— 2 6 0

Деление в восьмеричной системе близко делению в десятичной системе: нужно подобрать цифры частного. 232 делим на 54, в десятичной системе мы получили бы целое частное 4, но из предыдущего примера мы знаем, что в восьмеричной системе 54*4 = 260, это много, попробуем взять цифру поменьше – 3, умножаем 54*3 = 204, эта цифра подходит, и т.д.

В различных языках про­грам­мирования запись восьмеричных чисел начинается с 0, например, запись 011 означает десятичное число 9.

Ая система счисления

В шестнадцатеричной (hexadecimal) системе счисления применяются десять цифр от 0 до 9 и шесть первых букв латинского алфавита:

10 – A 11 – B 12 – C 13 – D 14 – E 15 – F.

При запи­си отрицательных чисел слева от последовательности цифр ставят знак ми­нус.

Для того чтобы при написании компьютерных программ отличить чис­ла, записанные в шестнадцатеричной системе, от других, перед числом ста­вят 0x. То есть 0x11 и 11 — это разные числа.

Шестнадцатеричная система счисления широко используется при зада­нии различных оттенков цвета при кодировании графической информации (модель RGB). Так, в редакторе гипертекста Netscape Composer можно зада­вать цвета для фона или текста как в десятичной, так и шестнадцатеричной системах счисления (см. рисунок).

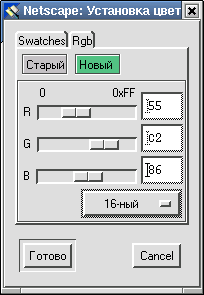
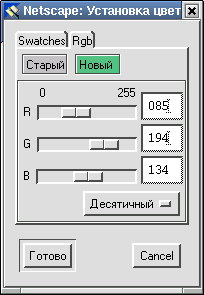
Пример выполнения операции сложения в 16-ой системе счис­ления:

1 1 Красным цветом показан перенос из младших разрядов

A 7 B₁₆ Выполнение операции в каждом разряде:

+ C 8₁₆ B + 8 = 11 + 8 = 19 = 1*16 + 3 = 13₁₆ (записываем 3)

B 4 3₁₆ 1+7+С = 8+12 = 20 = 1*16 + 4 = 14₁₆ (записываем 4)

Проверим результат путем перевода чисел в 10-ю систему:

A7B₁₆ = 10*16 2 + 7*16 +11 = 2683

B43₁₆ = 11*16 2 + 4*16 +3 = 2883

Пример выполнения операции вычитания в 16-ой системе счис­ления:

15 16 Красным цветом показан заем из старших разрядов

B 4 3₁₆ Выполнение операции в каждом разряде:

— A 7 B₁₆ 16 + 3 – B = 19 -11 = 8

C 8₁₆ 15 + 4 – 7 = 12 = C

Умножение и деление в 16-ой системе обычно не выполняется ввиду сложности вычислений.

Вернуться на главную страницу. или ЗАКАЗАТЬ РАБОТУ

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Преобразование десятичных чисел в двоичные
Допустим, нам нужно перевести число 19 в двоичное.
Вы можете воспользоваться следующей процедурой :

19 /2 = 9 с остатком 1
9 /2 = 4 c остатком 1
4 /2 = 2 с остатком 0
2 /2 = 1 с остатком 0
1 /2 = 0 с остатком 1
Итак, мы делим каждое частное на 2 и записываем в остаток 1 или 0. Продолжать деление надо пока в делимом не будет 1. Ставим числа из остатка друг за другом, начиная с конца. В результате получаем число 19 в двоичной записи (начиная с конца) : 10011.